Para entender como um Transformer funciona, vamos dissecar o diagrama abaixo que mostra todas as etapas do processo.
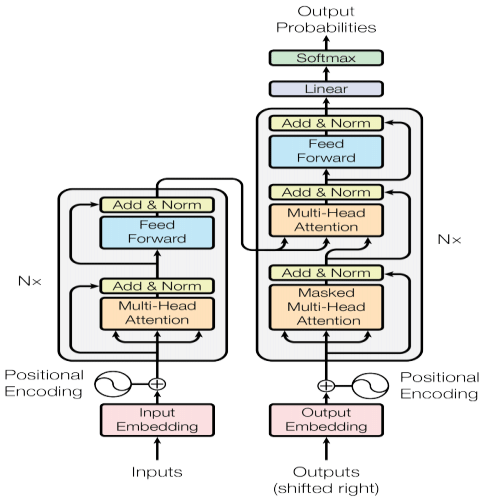
Input embeddings
Quando falamos no uso de redes neurais e mais amplamente técnicas de aprendizado de máquina trabalhamos exclusivamente com números. O que quero dizer com isso é que todo tipo de dado não estruturado, ou até mesmo estruturado, mas que esteja na forma de texto, por exemplo, tem que primeiro ser transformado em números para que possa ser “aprendido” pelos modelos de aprendizado de máquina.
Daí surge a questão: como transformar texto em números?
Bag of words
Existem algumas formas de fazer isso, e foram-se descobrindo novas alternativas para tentar resolver esse problema. Uma das primeiras soluções encontradas foi de dar uma “posição” a cada palavra e contar o número de aparições de cada uma das palavras no texto de entrada, a técnica chamada de bag of words . A imagem abaixo demonstra como isso é feito: cada palavra tem uma posição na tabela abaixo (cada palavra do vocabulário é uma coluna) e o valor de cada célula é a contagem de quantas vezes cada palavra apareceu no texto de entrada, representado pelas linhas.
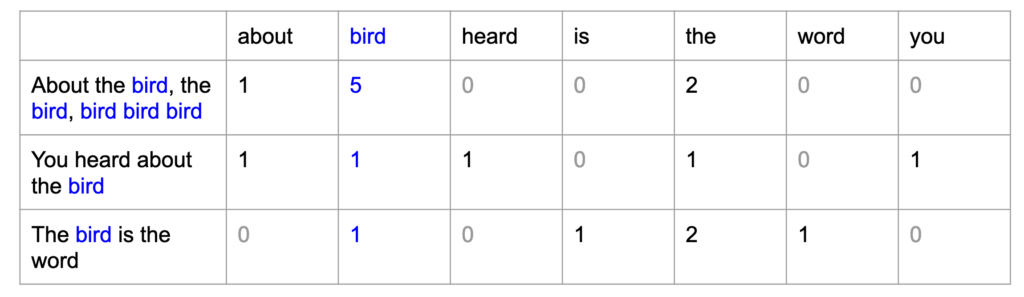
Uma característica dessa representação textual é que a matriz resultante é extremamente esparsa (palavra muito usada no contexto de aprendizado de máquina, nesse caso indica que existem muitos “0” na matriz). Pode-se imaginar que para contemplar a maior parte do vocabulário de uma língua, para que o modelo seja satisfatório, seria necessário muito mais colunas do que as representadas, sendo uma matriz de muitos “0” e apenas algumas colunas preenchidas com algum número. Como é de se imaginar, o “desperdício” computacional aqui é enorme, o português é uma língua com aproximadamente 370 mil palavras, imagine ter uma matriz de 370 mil (!) colunas para realizar os cálculos, e a maioria disso serem multiplicações por 0. Outra informação que é perdida aqui é a posição das palavras, algo que é extremamente importante para a interpretação de um texto. Pense nas seguintes frases: “Orlando é pai de Leandro” é completamente diferente de “Leandro é pai de Orlando” e as frases seriam representadas da mesma forma.
Daí pode surgir uma outra dúvida: por que não associar um identificador a cada palavra e ter uma matriz em que os valores são o índice (ou identificador de cada palavra) e as colunas serem a posição de cada palavra no texto, por exemplo? Pela natureza de redes neurais (e da maioria das técnicas de aprendizado de máquina) as features, no exemplo acima as colunas, são sempre variáveis quantitativas. Em outras palavras, se eu digo que a palavra “eu” tem o identificador 1 e a palavra “você” tem o identificador 2 isso não significa que “você” é maior que “eu”, pois apesar de 1 < 2, esses números são apenas identificadores, porém, um modelo “entenderia” que isso seria uma grandeza quantitativa, gerando uma confusão enorme e sendo impossível chegar em um resultado satisfatório para aplicações reais.
Palavras como vetores
Para resolver os problemas citados acima, algumas alternativas foram propostas com uma ideia principal em mente: palavras que aparecem juntas têm significados semelhantes e contextos semelhantes. A ideia aqui é que palavras podem ser representadas de acordo com n características arbitrárias. Para ilustrar essa ideia, temos o seguinte exemplo: a palavra “deságio” e a palavra “juros” são ambas palavras bastante utilizadas em contextos de textos financeiros, portanto, poderíamos definir uma grandeza quantitativa que seria o “financeirês”, ou seja, o quanto uma palavra é utilizada no contexto de textos financeiros, e teria seu domínio entre 0 e 1, quanto mais próximo de 1, mais essa palavra é utilizada nesses contextos. As duas palavras citadas certamente estariam próximas de 1, o que indica que se criássemos n grandezas, poderíamos classificar todas as palavras do vocabulário e palavras semelhantes teriam valores semelhantes para essas grandezas.
Nessa linha de pensamento surgem então algorítmos como o GloVe: Global Vectors for Word Representation, que representam palavras em n dimensões no espaço. Essas dimensões não tem nenhum significado que possa ser interpretado facilmente por nós seres humanos, como o “financeirês”, mas para os modelos esses significados existem.
Essa então é a primeira etapa de um Transformer e de grande importância! Nos vemos na próxima etapa, a de positional encoding.
