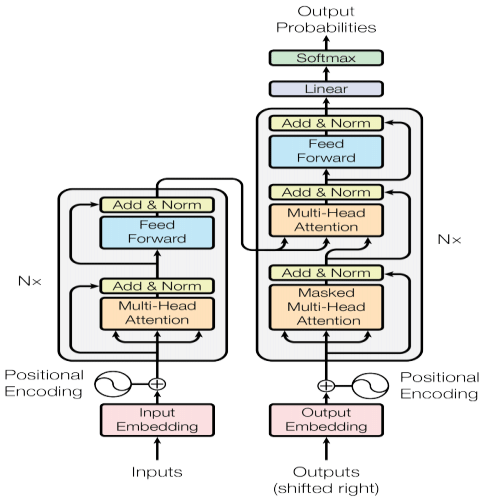
To understand how a Transformer works, let’s dissect the diagram below that shows all the steps in the process.
Input embeddings
When we talk about the use of neural networks and more broadly machine learning techniques, we work exclusively with numbers. What I mean by this is that any type of unstructured data, or even structured data, but in the form of text, for example, has to first be transformed into numbers so that it can be “learned” by machine learning models.
Hence the question arises: how to transform text into numbers?
Bag of words
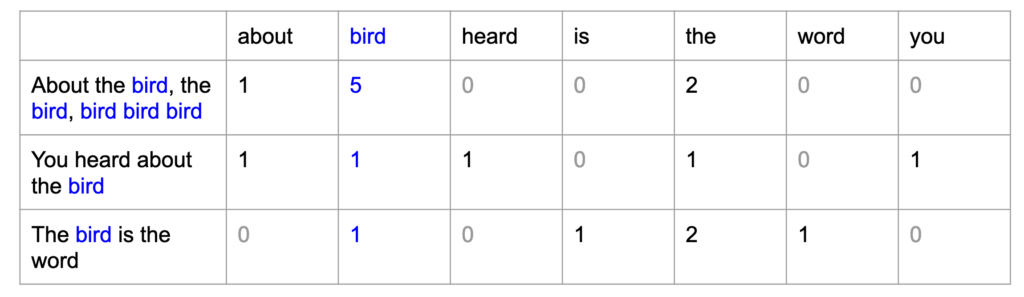
There are some ways to do this, and new alternatives have been discovered to try to solve this problem. One of the first solutions found was to give a “position” to each word and count the number of appearances of each word in the input text, a technique called bag of words. The image below demonstrates how this is done: each word has a position in the table below (each vocabulary word is a column) and the value of each cell is the count of how many times each word appeared in the input text, represented by the lines.
Then another question may arise: why not associate an identifier with each word and have a matrix in which the values are the index (or identifier of each word) and the columns are the position of each word in the text, for example? Due to the nature of neural networks (and most machine learning techniques) the features, in the example above the columns, are always quantitative variables. In other words, if I say that the word “I” has the identifier 1 and the word “you” has the identifier 2, this does not mean that “you” is greater than “I”, because despite 1 < 2, these numbers are just identifiers. However, a model would “understand” that this would be quantitative data, generating enormous confusion and making it impossible to arrive at a satisfactory result for real applications.
Words as vectors
To solve the problems mentioned above, some alternatives were proposed with one main idea in mind: words that appear together have similar meanings and similar contexts. The idea here is that words can be represented according to n arbitrary characteristics. To illustrate this idea, we have the following example: the word “taxes” and the word “interest” are both words widely used in contexts of financial texts, therefore, we could define a quantity that would be the “finance score”, that is, how much a word is used in the context of financial texts, and its domain would be between 0 and 1, the closer it is to 1, the more this word is used in this context. The two words mentioned would certainly be close to 1, which indicates that if we created n quantities, we could classify all words in the vocabulary and similar words would have similar values for these quantities.
In this line of thought, algorithms such as GloVe: Global Vectors for Word Representation emerge, which represent words in n dimensions in space. These dimensions do not have any meaning that can be easily interpreted by us human beings, such as “finance score”, but for models these meanings exist.
This is the first stage of a Transformer and of great importance! See you in the next step, positional encoding.
