Why transformers changed everything: before

In this series of articles I will discuss why the invention of transformers, published by the Google’s AI team in the paper titled Attention Is All You Need (2017) was so important to machine learning and the deep learning fields.

First of all, to understand the accomplishments of these proposed ideas, one must first understand how things were done before. We all know that context matters, in some cases, it matters a lot. For example, while reading this article, you keep all the text that came before in mind to comprehend the next sentences, otherwise it wouldn’t make any sense to you.

Of course, it doesn’t take long to one arrive to the conclusion that there can be a lot of concerns when dealing with context. Continuing with reading as an example, how long is your context? In other words, how many sentences (or ideas) back do you remember from a text in order to make sense of it? This answer cannot be other than that the context varies in length. So how can we input that into a model?

Using a neural network with words at their respective positions as input would not work as the model would have to have a fixed input size and we established that a context can’t have a fixed length. One of the first ideas was to use RNNs or Recurrent Neural Networks.

Recurrent Neural Networks

These are neural networks that look like this:

The h in the image is simply an activation function and weights. x are the inputs at each state and o is the prediction output for that state. The important thing to notice here is that the weights are equal between all the units of the network. This grants the following advantages to the model:

1. Information about past states is used by the network to calculate the output (prediction) of the model;
2. The quantity of past states can vary indefinitely;
3. The model is very computationally efficient and therefore are easily trained.

Unfortunately, although the advantages of this type of model seem great there are some deal-breaker problems with this approach:

1. The information from past several states is almost entirely lost and becomes practically unavailable at the last step of the calculation (the last layer);
2. This model suffers from the Vanishing/Exploding gradient problem.

These limitations restrict the use cases of this method to situations where the number of past states to be considered is relatively very small. However, the proposed architecture can be changed to fix these problems.

Vanishing/Exploding gradient problem

The vanishing/exploding gradient problem occurs because the inputs from preceding states are multiplied by the weights and pass through the activation function many times before reaching the final layer.

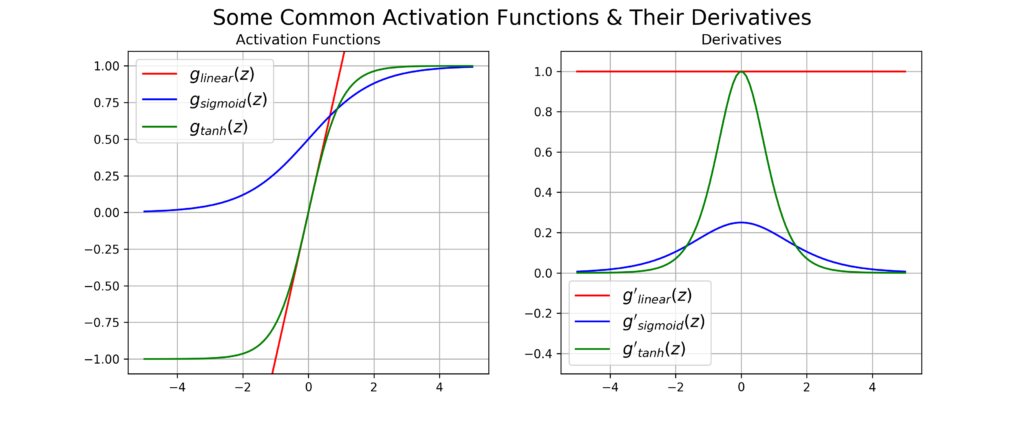
If we take a look at the activation functions and their derivatives in the image above we can see that on the positive and negative limits the derivatives go to zero, except for the linear function (that no one uses, because it doesn’t introduce nonlinearity to the model). This way, you can imagine that an input being multiplied many times by a single value and being passed many times through an activation function would have small final derivative.

Because the update of the weights depend on the partial derivative of the input, if it is too small, the updates become too small too and this hurts the model’s performance. The exploding gradient has more to do with the way the weights are initialized, they could grow very large and the updates can become so large that the model never converges.

Some solutions can be applied to solve the problem presented:

1. Use other activation functions, like ReLU. This activation function has a constant derivative, therefore, the gradient does not vanish (for a positive input);
2. Gradient clipping: threshold the gradient to a value;
3. Use Batch Normalization: this technique learns a normalization process to transform the output of each layer.

You can also try to change the model architecture to overcome this problem.

For the next article, I will be discussing the next architecture of Natural Language Models that came as an alternative to solve the problems imposed by the RNNs.